
The exact duration of the polishing stage is highly dependent on the surface specifications required. In this stage, the glass is rubbed against a polyurethane polisher wet with "slurry," an optical polishing compound typically comprised of water mixed with pumice or cerium oxide (Figure 2c). The third stage involves polishing the prism to the correctly specified surface flatness. In both the first two stages, the prism surface must be wet in order to expedite glass removal and prevent overheating of the glass itself. After smoothening, the glass surfaces should appear cloudy and opaque. Scratches left from the first stage are removed in the second stage (Figure 2b). Next is a fine grinding process that removes sub-surface breaks from the surface this stage is known as smoothening. At this point, the dimensions of the prism-to-be are very close to the desired specifications.
A majority of the glass is removed quickly in this stage resulting in flat, but still coarse surfaces (Figure 2a). This block is then ground, or generated, by a metal diamond bonded wheel into a near-finished product. In addition, most high precision prisms tend to be made in low quantities, meaning an automated process would be unnecessary.įirst, a block of glass (known as a "blank") of a specified grade and glass type is obtained. Due to the variability in shape, size, and, most importantly, the number of surfaces, a large-scale automated process for prism manufacturing is quite infeasible. In order to be used successfully in most applications, prisms must be manufactured with very strict tolerances and accuracies. PRISM MANUFACTURINGīefore delving into the theory behind prisms, consider their manufacturing process. Therefore, the substitution of one prism in lieu of several mirrors reduces potential alignment errors, increasing accuracy and minimizing the size and complexity of a system. Often, multiple mirrors are needed to achieve results similar to a single prism. Replacing mirror assemblies is perhaps the most useful application of prisms, since they both bend or fold light and change image parity. In all 3 of the above, we use the end polygon to calculate each of the faces, edges and vertices.A notable characteristic of prisms is their ability to be modeled as a system of plane mirrors in order to simulate the reflection of light within the prism medium. To calculate the number of vertices, we can say that it is the end polygon x 2 To calculate the number of edges, we can say it is the end polygon x 3 To calculate the number of faces, we can say that it is the end polygon + 2 If we have the end polygon, it will be easy to calculate the number of faces, vertices and edges of each 3D prism.

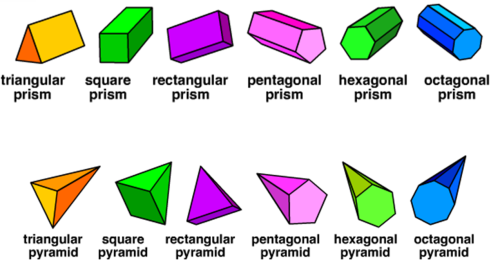
In the following table we can see the properties of 3D shapes that grade 7 learners must know: Irregular polygon:A polygon which has all its sides of unequal length and all its angles of unequal measures is called an irregular polygon.Ī scalene triangle is an example of an irregular polygon Regular polygon: A polygon which has all its sides of equal length and all its angles of equal measures is called a regular polygon.Īn equilateral triangle is an example of a regular polygon. If the end shape is not a regular polygon, we call in an irregular prism.Ī regular polygon has sides of equal length and an irregular polygon has sides of different length. If the end shape of the prism is a regular polygon, then we call the prism a regular prism. The cut you make, must be parallel to the ends of the prism. If you cut a prism along the length from one end to the other, it will have the same cross section along the whole length. The cross section of the shape stays the same and are called the ends of the prism or the base end. It has a pair of parallel faces, that are also congruent polygons. The prisms are a subclass of the prismatoids.Ī rectangular prism with 2 base ends and a cross sectionĪ prism is a 3D that has a constant cross section. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. All cross-sections parallel to the bases are translations of the bases. Source In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases.


 0 kommentar(er)
0 kommentar(er)
